1.
В XVI веке в Англии проживал известный придворный деятель и поэт сэр Уолтер Рэли. Знаменит он был, в первую очередь тем, что, однажды, бросил перед королевой в лужу свой дорогой плащ, чтобы Ее Величество на испачкало ног. Но нам он интересен не поэтому.
Была у сэра Уолтера Рэли страсть — очень он любил грабить испанские суда и искать Эльдорадо. И вот однажды увидел Рэли на корабле кучу сложенных ядер. И подумал (случалось такое с британскими придворными), мол, было бы неплохо, если бы можно было бы узнать, сколько ядер в куче, не пересчитывая их. Польза от такого знания, особенно если тебе нравится грабить испанский флот, очевидна.
Сам Рэли был в математике не очень, поэтому он задал эту задачку своему помощнику Томасу Хэрриоту. Тот, в свою очередь, был в математике силен (Хэрриот, кстати, является изобретателем знаков «>» и «<» для сравнения численных величин), поэтому довольно быстро решил эту задачу. Но Хэрриот был хорошим математиком, поэтому он задался вопросом: а как лучше всего укладывать ядра? Сам он немного подумал, но решить задачу не смог.
За комментариями он обратился к известному математику своего времени Иоганну Кеплеру — в то время помощнику Тихо Браге. Кеплер ответа не дал, но задачку запомнил. В 1611 году он опубликовал небольшую брошюрку, в которой обсуждал четыре вопроса: почему соты у пчел шестиугольные, почему лепестки цветов чаще всего группируются пятерками (Кеплер, вероятно, имел в виду толькорозовоцветных — прим. N + 1), почему зерна граната имеют форму додекаэдров (пусть и неправильных) и почему, наконец, снежинки имеют форму шестиугольников.
Брошюрка предназначалась в подарок, поэтому была скорее философским и развлекательным чтивом, нежели настоящей научной работой. Ответ на первый вопрос Кеплер связывал с двумя условиями — между сотами не должно быть пробелов, а сумма площадей ячеек должна быть минимальной. Второй вопрос автор связал с числами Фибоначчи, а разговор о снежинках натолкнул Кеплера на рассуждения об атомарных симметриях.
Третий же вопрос породил гипотезу о том, что гексагональная плотная упаковка (она на картинке ниже) является плотнейшей (что значит это в математическом смысле тоже ниже). Разумеется, на Хэрриота Кеплер сослаться не посчитал нужным. Поэтому это утверждение получило название гипотезы Кеплера. Закон Стиглера — он же принцип Арнольда — в действии.
Да, через 7 лет после выхода этой брошюрки сэру Уолтеру Рэли отрубили голову. Впрочем, с задачей о плотной упаковке это никак не было связано.
2.
По современным меркам задача, которую решал Хэрриот, была несложной. Поэтому разберем ее подробнее. А заодно и лучше поймем, как устроена гексагональная плотная упаковка.
Итак, главное условие, чтобы куча ядер не раскатилась во время качки. Итак, ыкладываем ядра в ряд на палубе. В следующий ряд кладем ядра так, чтобы шары размещались в щелях между сферами первого ряда. Если в первом ряду n шаров, то во втором n- 1 (потому что щелей между шарами на единицу меньше, чем самих шаров). Следующий ряд будет еще на единицу меньше ядер.
Те, кто помнит, что такое арифметическая прогрессия, легко сосчитают, что, если в первом ряду было n шаров, то всего в таком треугольнике n(n — 1)/2 шаров. Если смотреть сверху, то между шарами есть удобные выемки. Туда и будем складывать второй слой шаров. Получится треугольник, организованный как первый, только у которого на единицу меньше шаров в стороне. Значит, мы положили в кучу еще (n — 1)(n — 2)/2 шара.
Продолжим выкладывать слои до тех пор, пока не получим слой из одного шара. Получили треугольную пирамиду из ядер. Чтобы узнать, сколько в ней всего ядер, нужно сложить количества ядер в каждом слое. Если первый слой был со стороной n, то получим n слоев, которые в сумме дадут n(n + 1)(n + 2)/6. Пытливый читатель заметит, что это в точности биномиальный коэффициент C3n + 2. Это комбинаторное совпадение тут неспроста, но углубляться мы в него не будем.
Кстати, помимо этой задачи Хэрриот смог определить, какую примерно долю занимают ядра в достаточно большом контейнере, если принять форму последнего за куб. Оказалось, что доля составляет π/(3√2) ≈ 0,74048.
3.
Что значит слово плотнейшая в формулировке задачи? Рэли, Хэрриот, да и сам Кеплер не давали на это точного ответа. Подразумевалась плотнейшая в каком-то разумном смысле. Однако, для математики такая формулировка не подходит. Ее надо уточнить.
Читать дальше.
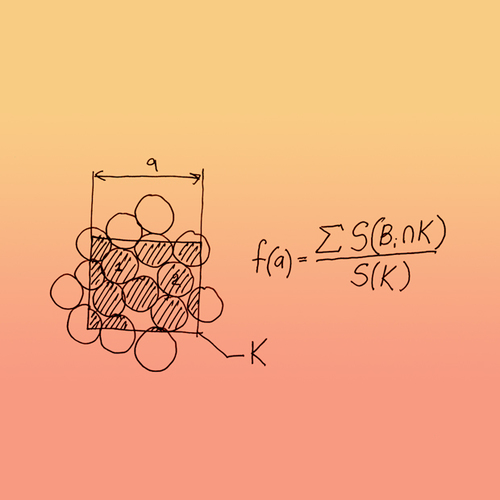
Комментарии:
Авторизуйтесь, чтобы оставить отзыв